Deeplearning 笔记：索引 切片 where,eye,reshape等函数,轴，秩的含义，整数数组索引

Posted on | In

2. Numpy

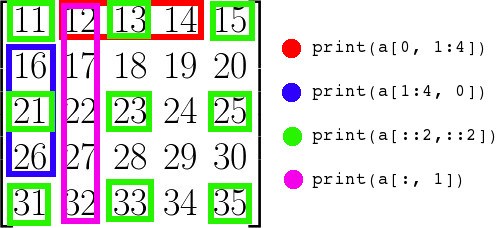
2.6 索引, 切片

1
2
3
4
5
6
7
8
9
10
>>> a
array([[ 0, 10, 20, 30, 40],
       [50, 60, 70, 80, 90]])
>>> b = a[0, 3] #第0行，第3列
>>> b
30
>>> c = a[1, 2] #第1行，第2列
>>> c
70
>>>
1
2
3
4
5
>>> a = np.array([[11, 12, 13, 14, 15],
              [16, 17, 18, 19, 20],
              [21, 22, 23, 24, 25],
              [26, 27, 28 ,29, 30],
              [31, 32, 33, 34, 35]])

2.7 where()函数，按照维度先后，列出满足条件的索引值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
>>> a = np.array([[11, 12, 13, 14, 15],
              [16, 17, 18, 19, 20],
              [21, 22, 23, 24, 25],
              [26, 27, 28 ,29, 30],
              [31, 32, 33, 34, 35]])
>>> b = np.where(a<=20)
>>> b #b的shape是(5, 5), 先按照第一个维度5行，第一行的索引都为0，从11-15都为0， 从16-20都为1
(array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1], dtype=int32), array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4], dtype=int32)) #再按照第二个维度5列，从11-15为0-4，从16-20为0-4组成一个2维数组
>>> c = np.where(a<=30)
>>> c
(array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3],
      dtype=int32), array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4],
      dtype=int32))
>>> d = np.where(a<=29)
>>> d
(array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3],
      dtype=int32), array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3],
      dtype=int32))
>>> e = np.where(a<=29)[0]
>>> e
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3],
      dtype=int32)

再看一个例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> a = np.arange(20)
>>> a = np.reshape(a, (2, 5, 2))
>>> a
array([[[ 0,  1],
        [ 2,  3],
        [ 4,  5],
        [ 6,  7],
        [ 8,  9]],

       [[10, 11],
        [12, 13],
        [14, 15],
        [16, 17],
        [18, 19]]])
>>> b = np.where(a<=13)
>>> b #第一维2，从0-9都为0， 10-19都为1。第二维5，0-1为0，2-3为1，4-5为2以此类推，10-11为0，12-13为1，第三维2，其中0,2,4,5,6,8,10,12为0，1,3,5,7,9,11,13为1，这样按照先后顺序组成一个3为数组。
(array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1], dtype=int32), array([0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 0, 0, 1, 1], dtype=int32), array([0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1], dtype=int32))
>>> np.shape(b)
(3, 14)

2.8 eye()函数

numpy.eye(N,M=None,k=0,dtype=<class 'float'>,order='C)返回的是一个二维的数组(N,M)，对角线的地方为1，其余的地方为0. 当M等于N时及相当于：identity(n,dtype=None)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
>>> import numpy as np
>>> a = np.eye(3) #M默认等于N,此例返回一个(3,3)的二维数组.k默认等于0表示主对角线，及第一个1的下标为0，往右移动为正，往左移动为负
>>> a
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
>>> b = np.eye(3, M=3, k=0) #等于a
>>> b
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
>>> c = np.eye(4, M=5, k=0) #主对角线
>>> c
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.]])
>>> c = np.eye(4, M=5, k=1) #k=1,向右移动一个位置
>>> c
array([[0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])
>>> d = np.eye(4, M=5, k=2) #k=2, 主对角线向右移动两个位置
>>> d
array([[0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.],
       [0., 0., 0., 0., 0.]])
>>> e = np.eye(4, M=5, k=3)
>>> e
array([[0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.]])
>>> f = np.eye(4, M=5, k=4)
>>> f
array([[0., 0., 0., 0., 1.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.]])
>>> g = np.eye(4, M=5, k=-1) #k=-1,主对角线想左移动一个位置
>>> g
array([[0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.]])
>>> h = np.eye(4, M=5, k=-2)
>>> h
array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.]])
>>> i = np.eye(4, M=5, k=-3)
>>> i
array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0.]])
>>> j = np.eye(4, M=5, k=-4) #k=-4,向左移出了范围，所以都为0
>>> j
array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.]])
>>>

2.9 reshape()参数中的-1

来源：https://www.zhihu.com/question/52684594/answer/297441394

举个简单的例子，要记住，python默认是按行取元素

1
c = np.array([[1,2,3],[4,5,6]])

输出：

[[1 2 3]
[4 5 6]]

我们看看不同的reshape

1
2
3
4
5
6
7
8
9
10
print '改成2行3列:'
print c.reshape(2,3)
print '改成3行2列:'
print c.reshape(3,2)
print '我也不知道几行，反正是1列:'
print c.reshape(-1,1)
print '我也不知道几列，反正是1行：'
print c.reshape(1,-1)
print '不分行列，改成1串'
print c.reshape(-1)

输出为：

改成2行3列:
[[1 2 3]
[4 5 6]]
改成3行2列:
[[1 2]
[3 4]
[5 6]]
我也不知道几行，反正是1列:
[[1]
[2]
[3]
[4]
[5]
[6]]
我也不知道几列，反正是1行：
[[1 2 3 4 5 6]]
不分行列，改成1串
[1 2 3 4 5 6]

一串是啥意思？一串就是秩rank()为0的矩阵～ (参看后面部分的3.0的解释)

2.10 NumPy中的维度(dimension)、轴(axis)、秩(rank)的含义

来源：https://zhuanlan.zhihu.com/p/51200424

在学习NumPy的时候，其中最重要的就是学习它的 ndarray 对象，它是多维度的同数据类型的数组。这个和Python自带的列表有较大的区别，列表中的元素类型是可以不相同的，如一个列表中，它可以包含数字、字符、字符串等，而在数组中，它的数据类型是相同的，如都是整型或者浮点型。

为什么Python中已经有了列表之后，在NumPy中还要引进一个数组对象呢？有以下三点可以作为参考，但在本文中不做具体描述：

  1. 数组对象可以去掉元素间运算所需的循环，使一维向量更像单个数据
  2. 设置专门的数组对象，经过优化，可以提升这类应用的运算速度
  3. 数组对象采用相同的数据类型，有助于节省运算和存储空间

NumPy中有几个概念比较绕，对于我来说比较难理解，因此以此文作为记录。它们分别是：维度、轴、秩。

对于维度的介绍，官网是这么写的“ In NumPy dimensions are called axes”，即维度称为轴。为了更直观的理解，可以将其与现实世界联系起来，比如在平面中即二维的世界中，我们描述一个点的时候，通常使用 x 轴、y 轴，这样就能确定一个点的具体位置了。因此，这里的两个维度，也就跟两个轴对应了起来。如果是立体的三维世界中，我们就会多出一个z轴，以此更加准确的来反映点的位置。所以，我么可以把以上的维度和轴进行等价。

什么是秩(rank)？它是指轴的数量，或者维度的数量，是一个标量

在下面的例子中，有一个数组 [1,2,1]， 它的维度是1，也就是有一个轴，这个轴的长度是3，而它的秩也为1。这些信息，都可以通过NumPy提供的数组属性来获得。

ndarray.ndim
the number of axes (dimensions) of the array
秩，数组轴的数量，或者维度的数量

ndarray.shape
the dimensions of the array. This is a tuple of integers indicating the size of the array in each dimension. For a matrix with n rows and m columns, shape will be (n,m). The length of the shape tuple is therefore the number of axes, ndim.
数组的维度。它的返回值是一个元组，这个元组描述了每个维度中数组的大小。相对于一个矩阵来说，shape表示的就是n行m列。这个元组的长度，等价于轴/维度的个数，即秩的值

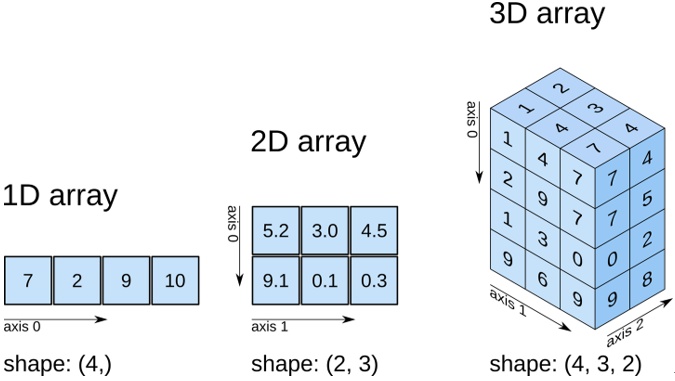
依旧以下图为例，我们已经知道数组a的维度数是1。查看它的shape，返回值为元组(3,) ，从这里也可以反映出这个数组的基本形状，即它是1维的，在这1维的空间中，拥有3个数据。

现在我们升级为一个2维的数组。如下图中的数组b，从属性 ndim 中可以知道，它的秩为2，即轴的个数是2，或者维度的数量是2（行和列两个维度）。shape中反映出来的是，它是2行3列的一个矩阵。

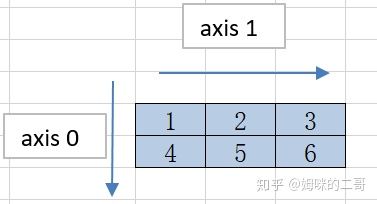
当前轴的数量已经上升为2，那么NumPy中是怎么定义这个轴的方向的呢？在二维中，轴0表示了数组的行，轴1表示了数组的列，见下方的示意图。因此，在该列中轴0的长度是2，轴1的长度是3。

如果我们把轴0上的数进行相加，可以得到一个一维数组，值为[5,7,9]，数组的元素个数为3。

如果我们把轴1上的数进行相加，也可以得到一个一维数组，但值为[6, 15]，数组的元素个数为2。

所以在不同轴上进行数据操作会得到不同的值，数组中的值是由沿轴方向上的数据相加所得。

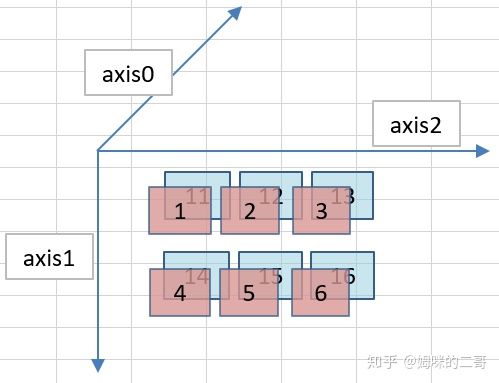
现在，我们再升级一个维度，使其成为一个3维数组，如下所示。秩的值已经变为3，它的shape反映出它的轴0长度为2，轴1长度为2，轴2的长度为3。

轴0-轴2，他们具体是怎么表现的呢？参见下面的图示，从图中可以看到，NumPy对于轴的编号由外向内，从行到列。

我们通过求和运算来验证上面轴方向的猜测是否正确。

先计算轴0上的数值，从示意图中看更像是，从表面到内部的一次“叠加”操作。这样计算后的一个结果，应该是一个2行3列的一个数组，形状如下：

[12, 14, 16]

[18, 20, 22]

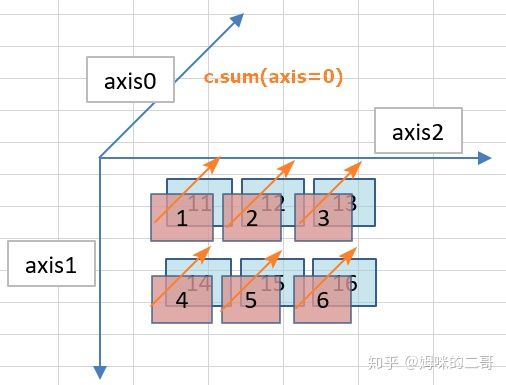
再计算轴1上的数值，从示意图中可以看出，这像是从上到下的一次“叠加”操作，计算后的值也是一个2行3列的新数组，形状如下：

[5, 7, 9]

[25, 27, 29]

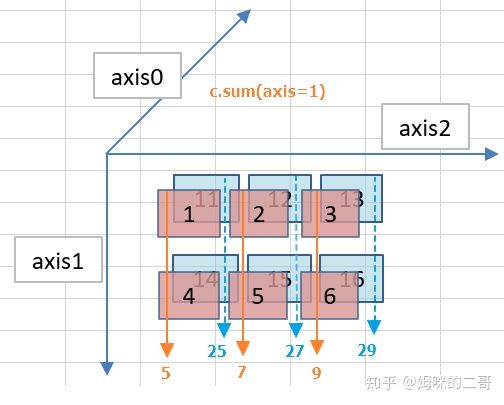
继续计算轴2上的数值，这次像是一次“右移叠加”的操作，形成的结果是一个2行2列的新数组，形状如下：

[6, 15]

[36, 45]

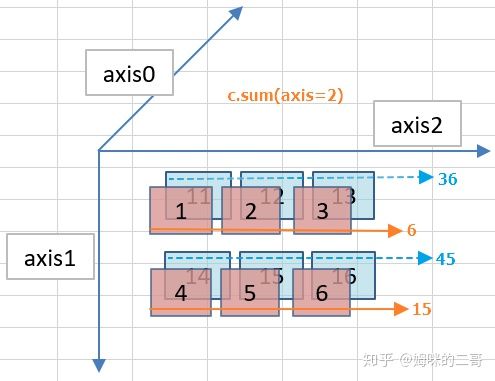
以下是运行结果，和我们的计算结果一致

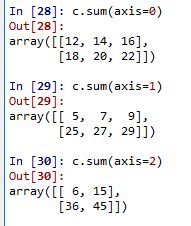
对于3维及更高维度的数组，理解及计算起来比较复杂。因此，我们也可以采用降维的方法来进行计算，如果维度降到二维，那么就非常便于我们的理解，简单的说就是“替换、降维打击”。

依旧以上面的三维数组c为例，我们只关心最外层的两个维度，将最内层维度的数据看成一个整体。

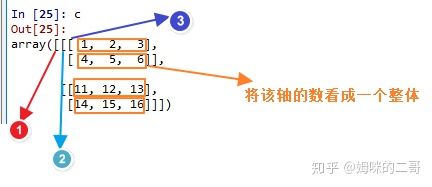
转化后的形状就如下图所示，这时我们计算轴0就等于计算 A+C，B+D；计算轴1就等于计算 A + B，C + D

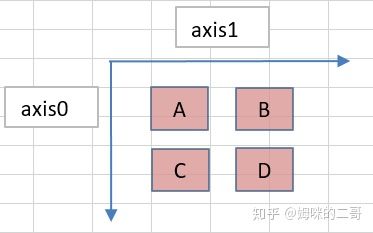
运行结果如下所示

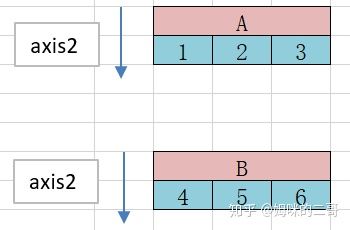
轴2要怎么计算呢？由于我们上面已经将最内层的数组看成了一个整体，如图所示。所以，我们计算轴2，就等同于对数组 A、B、C、D进行分别求和

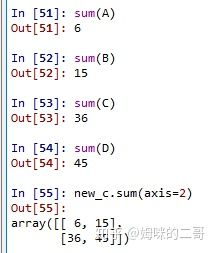
2.11 整数索引与切片索引混合使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> a #a是(4, 5)两个维度
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
>>> b = a[1:3, 3] #整数索引与切边索引混用会产生一个低维度的数组
>>> b
array([ 8, 13])
>>> b.shape #b是一个维度
(2,)
>>> c = a[1:3, 3:4] #而只是用切片索引，会产生同原始数组一样维度的数组
>>> c
array([[ 8],
       [13]])
>>> c.shape
(2, 1)
>>>

继续看一个例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> b
array([ 8, 13])
>>> c
array([[ 8],
       [13]])
>>> a[1, 3]
8
>>> a[1, 3] = 88 #修改a数组的一个元素，b,c对应的元素也会一起改变。据说是共用统一内存的原因
>>> a
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7, 88,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
>>> b
array([88, 13])
>>> c
array([[88],
       [13]])
>>>

2.12 整数数组索引

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> a
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7, 88,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
>>> a[[0, 1, 2], [0, 1, 2]] #整数数组通过每个维度分别定位，第一个维度[0, 1, 2]0行，1行，2行，然后分别对应相应的列0行的0列，1行的1列，2行的2列
array([ 0,  6, 12])
>>> np.array([a[0, 0], a[1, 1], a[2, 2]])
array([ 0,  6, 12])
>>> a[[3, 3], [4, 4]] #同理对应3行的4列 和 3行的4列
array([19, 19])
>>> np.array([a[3, 4], a[3, 4]])
array([19, 19])
>>> a[[0, 1, 2], [0, 1, 2]] += 10 #可以快速的计算
>>> a
array([[10,  1,  2,  3,  4],
       [ 5, 16,  7, 88,  9],
       [10, 11, 22, 13, 14],
       [15, 16, 17, 18, 19]])