Deeplearning 笔记：meshgrid函数 梯度

Posted on | In

2.Numpy

2.18 meshgrid函数

参考文章Numpy中Meshgrid函数介绍及2种应用场景

[xv,yv] = meshgrid(x,y) 将向量x和y定义的区域转换成矩阵xv和yv,其中矩阵xv的行向量是向量x的简单复制，而矩阵yv的列向量是向量y的简单复制(注：下面代码中xv和yv均是数组，在文中统一称为矩阵了)。假设x是长度为m的向量，y是长度为n的向量，则最终生成的矩阵xv和yv的维度都是 nm （注意不是mn）。

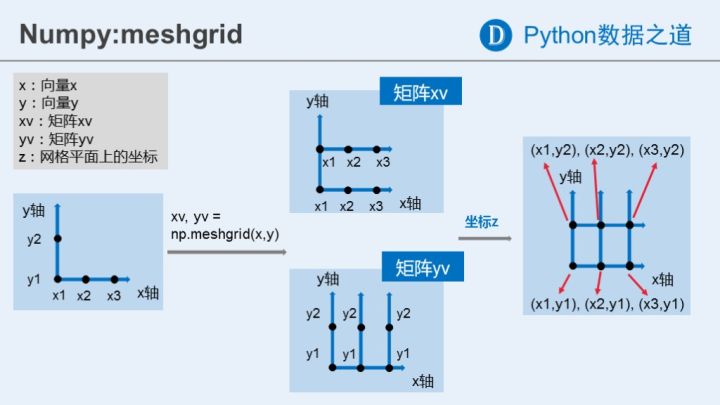
参考上图再看下面的代码，x, y为一维数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
>>> x = np.arange(3)
>>> x
array([0, 1, 2])
>>> y = np.arange(2)
>>> y
array([0, 1])
>>> xv, yv = np.meshgrid(x, y)
>>> xv #x保持横轴数据不变，在纵轴上复制的次数为y的数据个数，本例中为复制2次
array([[0, 1, 2], #最终得到的数组shape都为(2, 3)
       [0, 1, 2]])
>>> yv #如下保持数据在纵轴上的不变，复制的次数为x的数据个数，本例为复制3次
array([[0, 0, 0],
       [1, 1, 1]])
>>> z = [i for i in zip(xv.flat,yv.flat)]
>>> z
[(0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1)]
>>> x.shape
(3,)
>>> y.shape
(2,)
>>> xv.shape
(2, 3)
>>> yv.shape
(2, 3)
>>>

4. Deep Learning From Scratch

4.2 函数求导

教材中求f(x)=0.01x**2 + 0.1x，当x=5时的导数，以及它的切线函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt

#求f(x)的导数，f为函数
def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

#要求导数的函数f(x)
def function_1(x):
    return 0.01*x**2 + 0.1*x 

#求x在f(x)上的导数，以及对应的切线函数.下面的推导过程参考下面的图片
def tangent_line(f, x):
    d = numerical_diff(f, x)
    print(d)
    y = f(x) - d*x #y为切线函数与纵轴的交点。我不是非常理解为什么是f(x)-d*x而不是后者减去前者，这个正负问题。
    return lambda t: d*t + y
     
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")

tf = tangent_line(function_1, 5)
y2 = tf(x)

plt.plot(x, y)
plt.plot(x, y2)
plt.show()

推导过程：

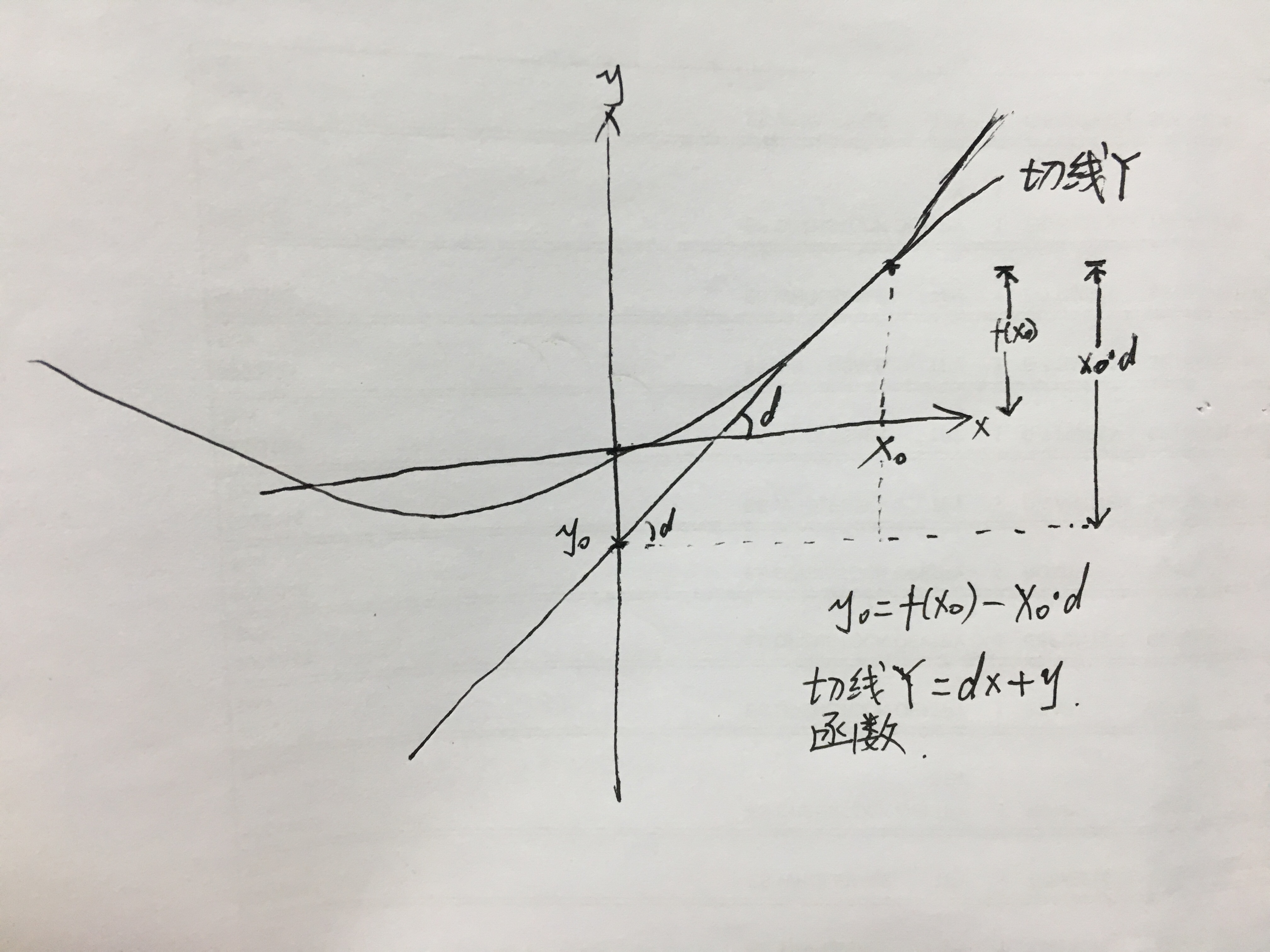
4.3 梯度

这段代码，我主要分析了梯度的计算过程，而没有分析它绘图的过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
# coding: utf-8
# cf.http://d.hatena.ne.jp/white_wheels/20100327/p3
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

#求一维数组在函数中的导数
def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x) #生成一个同x形状，元素全为0的数组，grad同x在这里是一维数组
    
    for idx in range(x.size): 
        tmp_val = x[idx] #导出一维数组中每个元素并赋值给tmp_val
        x[idx] = float(tmp_val) + h #然后再在这个元素上加上一个微小数，并修改x数组的对应元素
        fxh1 = f(x) # f(x+h) #把x数组代入f(x)函数中得到一个值
        
        x[idx] = tmp_val - h #同理求出同一元素减去微小数后数组的代入函数后得到的值
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h) #得到一个导数，再导入grad同一位置。
        
        x[idx] = tmp_val # 还原值 #将x还原
        
    return grad #这样得到每个元素对应的导数组成的一维数组

#2维数组在函数f的求导
def numerical_gradient(f, X):
    if X.ndim == 1: #如果参数X是一维数组
        return _numerical_gradient_no_batch(f, X) #求一维数组的导数
    else:
        grad = np.zeros_like(X) #如果是2维数组，则grad生成对应的元素为0的2维数组
        
        for idx, x in enumerate(X): #idx为列的下标，x为idx列下标下每一行的数组为一维数组
            grad[idx] = _numerical_gradient_no_batch(f, x) #每一行的数组生成对应的导数组成的一维数组，再导入grad对应下标列的每行
        
        return grad #最终得到一个完整的2维数组

#函数
def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else: #2维数组中求横轴方向的数组平方和
        return np.sum(x**2, axis=1)

#求x在函数中的导数和对应的切线函数，在这段代码中似乎没有用上
def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y
     
if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1) #参考文章前面meshgrid函数，x0, y0均为一维数组，shape均为(18, ),所以X, Yshape均为(18, 18)二维数组
    
    X = X.flatten() #把X, Y分别改写为一维数组
    Y = Y.flatten()
    
    grad = numerical_gradient(function_2, np.array([X, Y]) ) #这里np.array([X, Y])是二维数组
    
    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    plt.show()

后记：

1.最近业余时间带小孩，电脑又罢工了一段时间，学习进度变得很慢。

2.感觉数学知识越来越多了，越来越复杂了。

3.还得一步一个脚印向前走。